Alles begint met het architectuurmodel en de schematisering
Als stabiliteitsingenieur, krijgen we de opdracht om een constructie te berekenen zodat die niet bezwijkt. We moeten controleren of de constructie voldoet aan bepaalde eisen qua sterkte, stabiliteit en stijfheid. Voor het maken van het analyse model, vertrekken we van het architectuurmodel. Een architectuurmodel geeft weer hoe de structuur er in werkelijkheid zal uitzien, maar is niet geschikt voor berekeningen door de vele details.
We zullen het architectuurmodel moeten strippen totdat enkel de draagstructuur overblijft. De draagstructuur zal de aangrijpende belastingen herleiden naar de grond. Mogelijke aangrijpende belastingen zijn het gewicht van de constructie zelf, gewicht resulterend uit het gebruik van de constructie (mensen, meubilair, machines). Maar ook wind, sneeuw, temperatuursveranderingen, … kunnen ook voor belastingen zorgen en moeten dus in rekening worden gebracht.
Om de draagstructuur toegankelijk te maken voor berekeningen, moeten we het schematiseren naar een analyse model (syn.: reken model, mechanica model) van maken. Dit gaat gepaard met noodzakelijke idealiseringen en vereenvoudigen om het krachtenspel in de constructie te kunnen weergeven. De idealiseringen zitten op gebied van:
• De geometrie (de vorm en afmetingen) van de structuur
• De opleggingen
• De verbindingen
Figuur 1: Schematisering van een architectuurmodel (a) naar een analyse model (b)
Vorm van de structuur
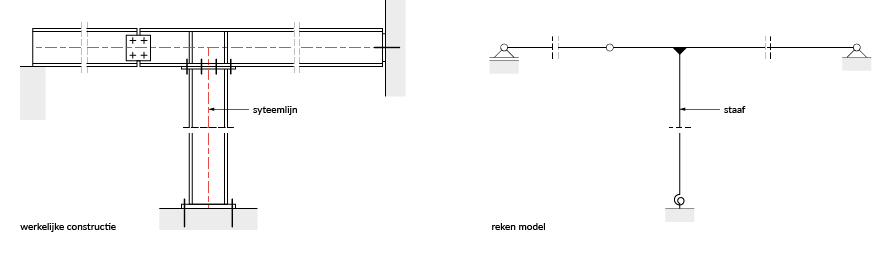
Door de schematisering, zullen systeemlijnen die samenvallen met de assen van de doorsnede de balken en kolommen vervangen. Analoog, zullen systeemvlakken die samenvallen met het asvlak de vloeren en wanden vervangen.
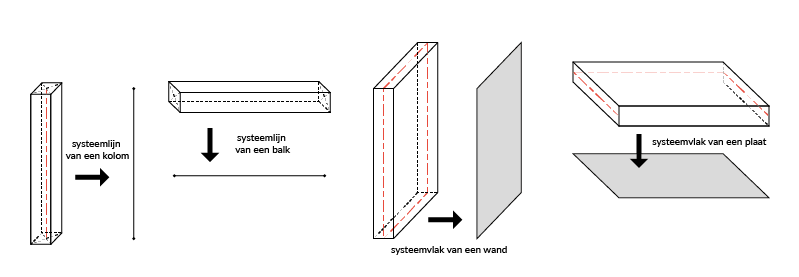
Figuur 2: Schematisering van een balk/ kolom (a) en van een plaat/wand (b) naar respectievelijk systeemlijnen en -vlakken
Doordat we met systeemlijnen en -vlakken werken, is de rekenwaarde van de overspanningen in een analysemodel een klein beetje verschillend van de werkelijke afmetingen die we terugvinden in de werkelijke constructie (= architectuurmodel). In Figuur 3 zijn:
• de balken in het analyse model iets korter dan in werkelijkheid
• de kolommen iets langer dan in werkelijkheid
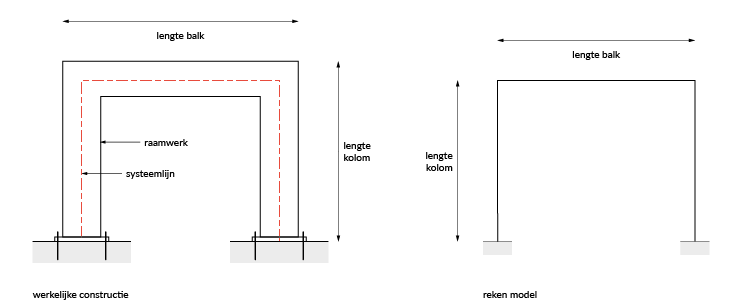
Figuur 3: Invloed van de schematisering op de lengte van constructieonderdelen
Zodra de positie van de systeemlijnen en -vlakken bepaald is, moeten we hieraan een doorsnede toekennen. Hoe beter deze initiële keuze aansluit bij het finaal ontwerp, hoe minder rekenwerk. Als richtlijn, kunnen we onderstaande vuistregels gebruiken om de initiële doorsnede van elk element te schatten.
| Vloerliggers | ||
|---|---|---|
| Beton | Ter pl. gestort | L/10 |
| Préfab | L20 | |
| Staal | L/20 | |
| Hout | gezaagd | L20 |
| gelamineerd | L12 | |
| Dakliggers | ||
| Beton | Ter pl. gestort | L/20 |
| Préfab | L20 | |
| Staal | L/30 | |
| Hout | gezaagd | L20 |
| gelamineerd | L20 | |
| Kolommen | ||
| Beton | 1 bouwlaag (L<=8m) | L/12 à L/15 |
| Meerdere bouwlagen (L <= 4m) | L/10 à L/12 | |
| Staal | 1 bouwlaag (3m <= L<= 8m) | L/20 à L/25 |
| Meerdere bouwlagen (3m <= L<= 4m) | L/7 à L/8 | |
| Hout | 1 bouwlaag | L/20 |
| Vloeren in beton | ||
| Lijnondersteuning (tot 7m) | Enkel veld | 1/22 |
| Doorgaand | 1/30 | |
| Puntvormige ondersteuningen (tot 7m) | 1/25 à 1/28 | |
| Casettevloer, holle vloer, ribbenvloer (tot 20m) | 1/20 à 1/25 x lengte diagonaal | |
| Welfsel (tot 17m) | L/35 | |
| TT-vloer (tot 22m) | L/30 | |
Tabel 1: Vuistregels voor het schatten van dimensies van constructie onderdelen (Bron: [4])
Opleggingen en verbindingen
Een constructie(deel) zweeft niet vrij in de lucht. Constructiedelen zijn onderling met elkaar verbonden in verbindingen (syn. knopen – vooral in de staalbouw). En de constructie in z’n geheel, is verbonden aan deze planeet via opleggingen (syn. ondersteuningen, steunpunten) die de interne krachten afleiden naar de grond.
De schematisering van opleggingen/ knopen hangt af van hun mogelijke bewegingsvrijheid. Die bewegingsvrijheid speelt op twee niveaus:
• Enerzijds is de translatiestijfheid een maat voor de weerstand van de oplegging/verbinding tegen verplaatsingen.
• En anderzijds is de rotatiestijfheid is een maat voor de weerstand van de oplegging/ verbinding tegen verdraaien.
Een oplegging/ verbinding beperkt steeds minstens één vrijheidsgraad. In een tweedimensionaal plat vlak heeft een oplegging/verbinding maximaal 3 vrijheidsgraden: twee translaties en één rotatie (Figuur 4).
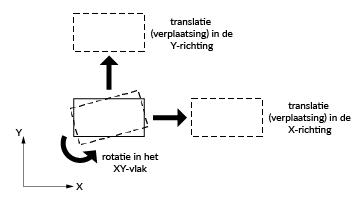
Figuur 4: De drie vrijheidsgraden in een tweedimensionaal plat vlak geïllustreerd met een rechthoek (Bron: [3])
Door te spelen met de translatie- en rotatiestijfheid, kunnen we verschillende opleggingen/ verbindingen onderscheiden (Figuur 5).
• Het scharnier, de rol en de inklemming zijn de meest gebruikte opleggingen. Hierbij is zowel de translatie- als rotatiestijfheid belangrijk.
• Om verbindingen te classificeren, wordt meestal enkel gebruikt gemaakt van de rotatiestijfheid.
o Verbindingen met een vrije rotatie worden scharnierende verbindingen genoemd.
o Verbindingen waarin de rotatie verhinderd is, worden stijve, vaste of continue verbindingen genoemd.
o Verbindingen met een beperkte rotatiestijfheid, worden half-stijve verbindingen genoemd.
Figuur 5: Mechanische voorstelling van diverse opleggingen/verbindingen i.f.v. hun translatie- en rotatiestijfheid (Bron: [3])
Bij het maken van een analyse model moeten we dus de opleggingen en verbindingen zodanig schematiseren zodat die zo goed mogelijk het reële gedrag benaderen. In Figuur 6 zie je dezelfde constructie als in Figuur 1, maar dit keer zijn de opleggingen en verbindingen getoond samen met hun respectievelijke schematisering. Zo wordt bijvoorbeeld de vrije oplegging uit het werkelijke model vertaalt naar een roloplegging in het analyse model. Of de flexibele kolom-voetplaat verbinding naar een verende inklemming, enzo verder.
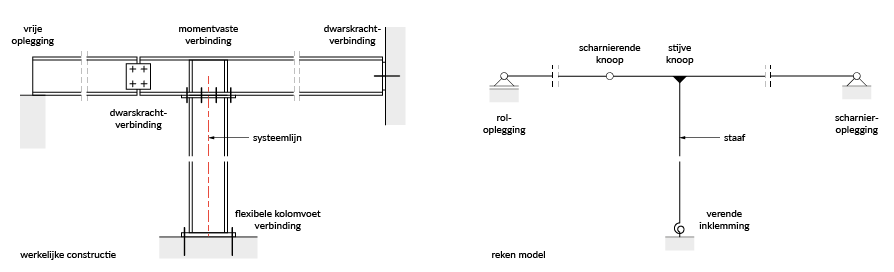
Figuur 6: Schematisering van de opleggingen en knopen in een constructie
Onderstaande tabel toont foto’s van werkelijke opleggingen/verbindingen en hun bijhorende schematisering.
| Voorbeelden van opleggingen | Voorbeelden van knopen | ||
|---|---|---|---|

| Tussen een prédal en een dragende muur wordt een neopreen strip gelegd. De neopreen strip zorgt ervoor dat de prédal kleine horizontale verplaatsingen kan ondergaan. |  | Klassieke geboute balk-kolom verbinding met kniestuk. Het kniestuk zorgt voor extra rotatiestijfheid.
|
 | Schematisering: roloplegging | Schematisering: stijve verbinding | |
 | Zowel alle translaties als rotaties zijn verhinderd in deze oplegging. |  | Balk-kolom verbinding in beton waarbij de balk wordt opgelegd op een console. Meestal kan deze verbinding geen moment overdragen. |
Schematisering: inklemming | 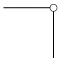 | Schematisering: scharnierende verbinding | |
 | De vier bouten zorgen ervoor dat deze oplegging een zeker momentweerstand kan ontwikkelen. Helaas is deze weerstand niet van dezelfde grootorde als bij een inklemming. |  | Een balk-balk verbinding in beton. Ook wel een tandoplegging genoemd. Deze verbinding kan geen moment overdragen |
| Schematisering: verende inklemming | Schematisering: scharnierende verbinding | ||
 | Enkel in de bruggenbouw kom je de opleggingen in hun zuiverste vorm tegen. Dit voorbeeld is een scharnieroplegging. De translaties zijn verhinderd, maar de rotatie kan ongehinderd optreden. |  | Een geboute balk-kolom-balk verbinding zonder kniestukken. Deze verbinding heeft een zekere rotatiestijfheid maar niet van dezelfde grootorde als wanneer er kniestukken aanwezig zouden zijn. |
| Schematisering: scharnierende oplegging | 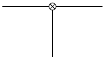 | Schematisering: half-stijve verbinding | |
Indien een bepaalde vrijheidsgraad (translatie of rotatie) vrij of verhinderd is, is het mechanica model van de oplegging/knoop snel bepaald. Het is alles of niets. Maar met translatieveren en rotatieveren is dat een ander verhaal. Er bestaan binnen de structurele analyse een aantal manieren om de waarde van die translatie- en rotatieveren te bepalen. Het is echter buiten de scope van dit artikel om daar verder op in te gaan.
Praktische toepassing: analyse model in Diamonds
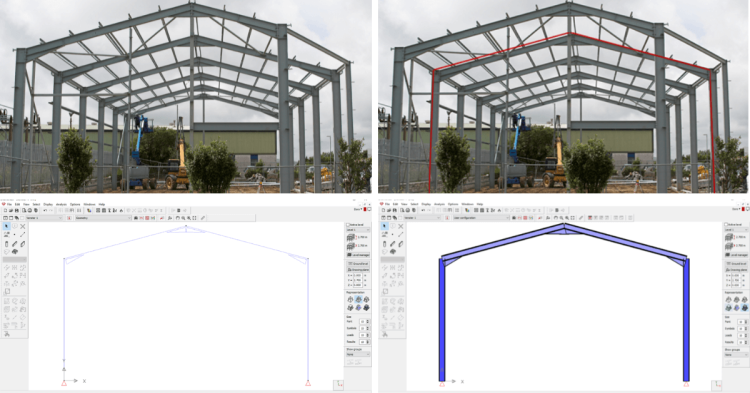
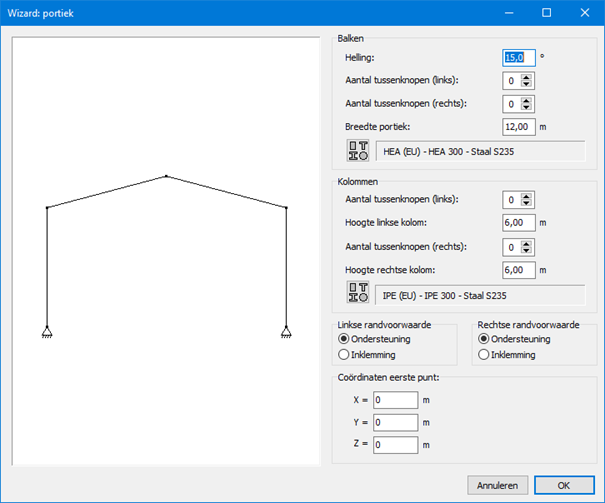
Laat ons deze kennis nu een toepassen in Diamonds, ons meest uitgebreide programma voor structurele analyse. We maken het analyse model voor het tweede spant uit onderstaande hal.

De afmetingen van de systeemassen zijn als volgt:
• Breedte: 12m
• Kolom hoogte: 6m
• Dakhelling: 15°
Om beter te begrijpen waar de systeemassen precies liggen, tekenen we ze op de foto:

Aan de systeemassen moeten we profielen toekennen. Op basis van Tabel 1, kunnen we een eerste inschatting maken:
• Kolommen: 6000mm/ 20 = 300mm > HEA 300
• Balken: 6000mm/ 20 = 300mm > IPE 300
• Kniestuk: lengte 1m, hoogte gelijk aan de IPE-hoogte waarop het kniestuk bevestigd wordt.
• Opleggingen: neem aan scharnierend
• Verbindingen: vaste verbindingen (door aanwezigheid kniestuk). Verbindingen zijn default vast in Diamonds.
Om snel een spantje te genereren, maken we gebruik van de structuur generator.

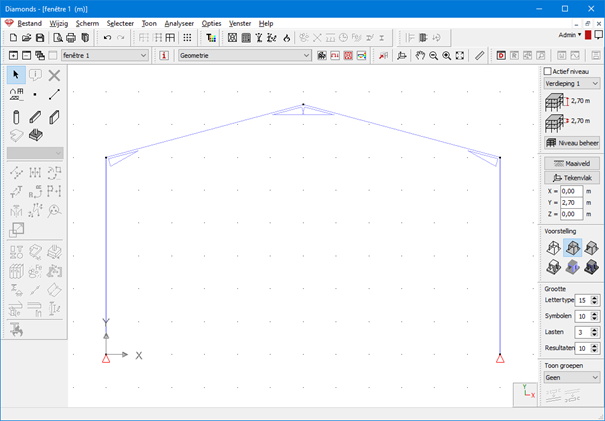
In bovenstaande afbeelding wordt het spant afgebeeld in een draadvoorstelling: enkel de systeemassen zijn zichtbaar. Vragen we een massieve voorstelling, dan worden de profiel afmetingen gegenereerd en op de systeemassen geplakt. Dit heeft als gevolg dat deze voorstelling er niet uitziet zoals de werkelijke constructie (= architectuurmodel):
• Balken en kolommen lijken niet mooi aan te sluiten.
• Ook de balk-balk verbinding in de nok lijkt niet mooi aan te sluiten.
• De kniestukken in de nok overlappen (dat is zelfs al te zien in het draadmodel).
Maar deze zaken zijn normaal. Ze zijn het gevolg van de schematisering van een architectuurmodel (dat niet vatbaar is voor berekeningen) naar een analyse model (dat wel vatbaar is voor berekeningen).
Diamonds – productieve software voor berekening van constructies
Maak het waar met Diamonds, de beste keuze van construcief ingenieurs! Probeer het zelf.
Literature:
1. Braam, R., & Lagendijk, P. (2010). Constructieleer gewapend beton (7de editie). Vrije Uitgevers, de.
2. Stark, J., & Wardenier, J. (2014). Knopen (1ste editie). Bouwen Met Staal.
3. Dicke, D. (1991). Stabiliteit voor ontwerpers (2e druk). Delftse U.M.
4. Vuistregels voor het ontwerpen van een draagconstructie. (2013, 20 november). Wiki BK TU Delft. Geraadpleegd op 19 januari 2021, van http://wiki.bk.tudelft.nl/mw_bk-wiki/images/1/12/Vuistregels.pdf
5. Hanaor, A. (1998). Principles of Structures. Blackwell Publishing.
